Triangle
Formules de résolution autour d'un triangle
Résolution d'un triangle rectangle
A
B
C
acN = (c - a).GetNormalized()
bc2 = (c - b).GetLengthSquared()
ac = (c - a).GetLength()
co = bc2 / ac
d = c + acN * coCopie du troisième point d'un triangle
A
B
C
D
E
UP
ac = c - a
ab = b - a
abN = ab.GetNormalized()
dotH = ac.Dot(abN)
h = (abN * dotH) + a
de = e - d
deN = de.GetNormalized()
fac = de.GetLength() / ab.GetLength()
h2 = deN * (dotH * fac) + d
ch = h - c
hcL = ch.GetLength()
deVec = deN.Cross(up)
abVec = ab.Cross(up)
if (abVec.Dot(ch) > 0) {
fac = -fac
}
f = deVec * (fac * hcL) + h2Calcul d'un point dans un quadrangle en fonction des coordonnées barycentriques
A
B
C
D
i
j
o = (c - d - b + a) * (i * j) + (d - a) * j + (b - a) * i + a
e = (b - a) * i + a
g = (c - d) * i + d
f = (c - b) * j + b
h = (d - a) * j + aCalcul des coordonnées barycentriques dans un quadrangle à partir d'un point (coordonnées de Wachspress)
A
B
C
D
O
i
j
delta A
delta B
delta C
delta D
function aireTriangle(a, b, c) {
return (a - b).Cross(a - c).GetLength() * 0.5;
}
#
# Cas où O est connu
#
aireAOB = aireTriangle(a, o, b)
aireAOD = aireTriangle(a, o, d)
aireDOC = aireTriangle(d, o, c)
aireBOC = aireTriangle(b, o, c)
#
aireDAB = aireTriangle(d, a, b)
aireABC = aireTriangle(a, b, c)
aireBCD = aireTriangle(d, b, c)
aireCDA = aireTriangle(c, d, a)
#
da = aireDAB / (aireAOD * aireAOB)
db = aireABC / (aireAOB * aireBOC)
dc = aireBCD / (aireBOC * aireDOC)
dd = aireCDA / (aireDOC * aireAOD)
#
let tot = da + db + dc + dd
#
deltaA = da / tot
deltaB = db / tot
deltaC = dc / tot
deltaD = dd / tot
#
i = deltaB + deltaC
j = deltaC + deltaD
#
# Cas où on cherche O
#
o = a * deltaA + b * deltaB + c * deltaC + d * deltaDCalcul des coordonnées barycentriques dans un triangle à partir d'un point
A
B
C
O
delta A
delta B
delta C
function determinant(v1, v2) {
return v1.x * v2.z - v1.z * v2.x
}
#
# Cas où O est connu
#
ab = b.moins(a)
ac = c.moins(a)
ao = o.moins(a)
det = determinant(ab, ac)
#
deltaB = determinant(ao, ac) / det
deltaC = determinant(ab, ao) / det
deltaA = 1 - deltaC - deltaB
#
# Cas où on cherche O
#
o = a * deltaA + b * deltaB + c * deltaC Dépliage
Dépliage


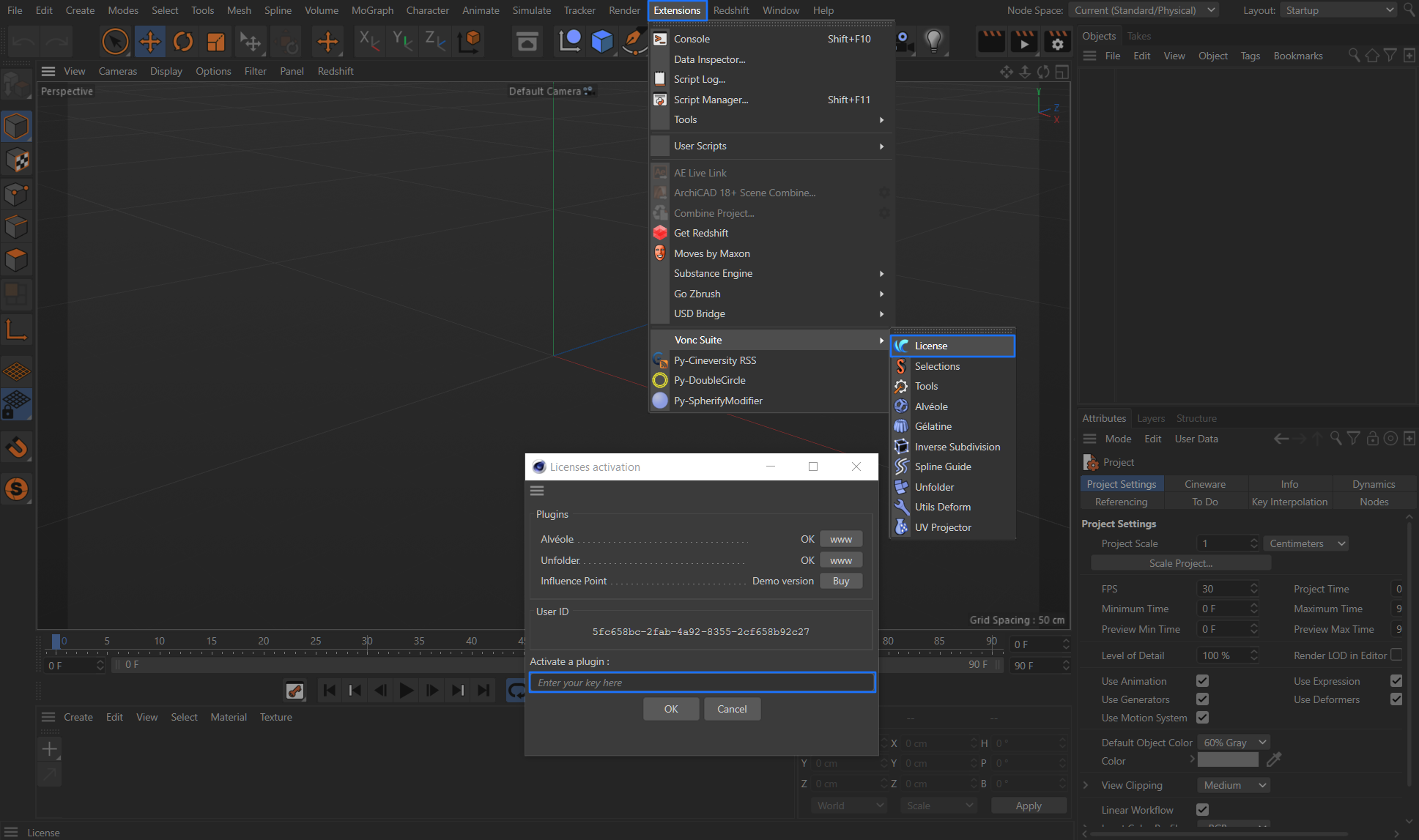
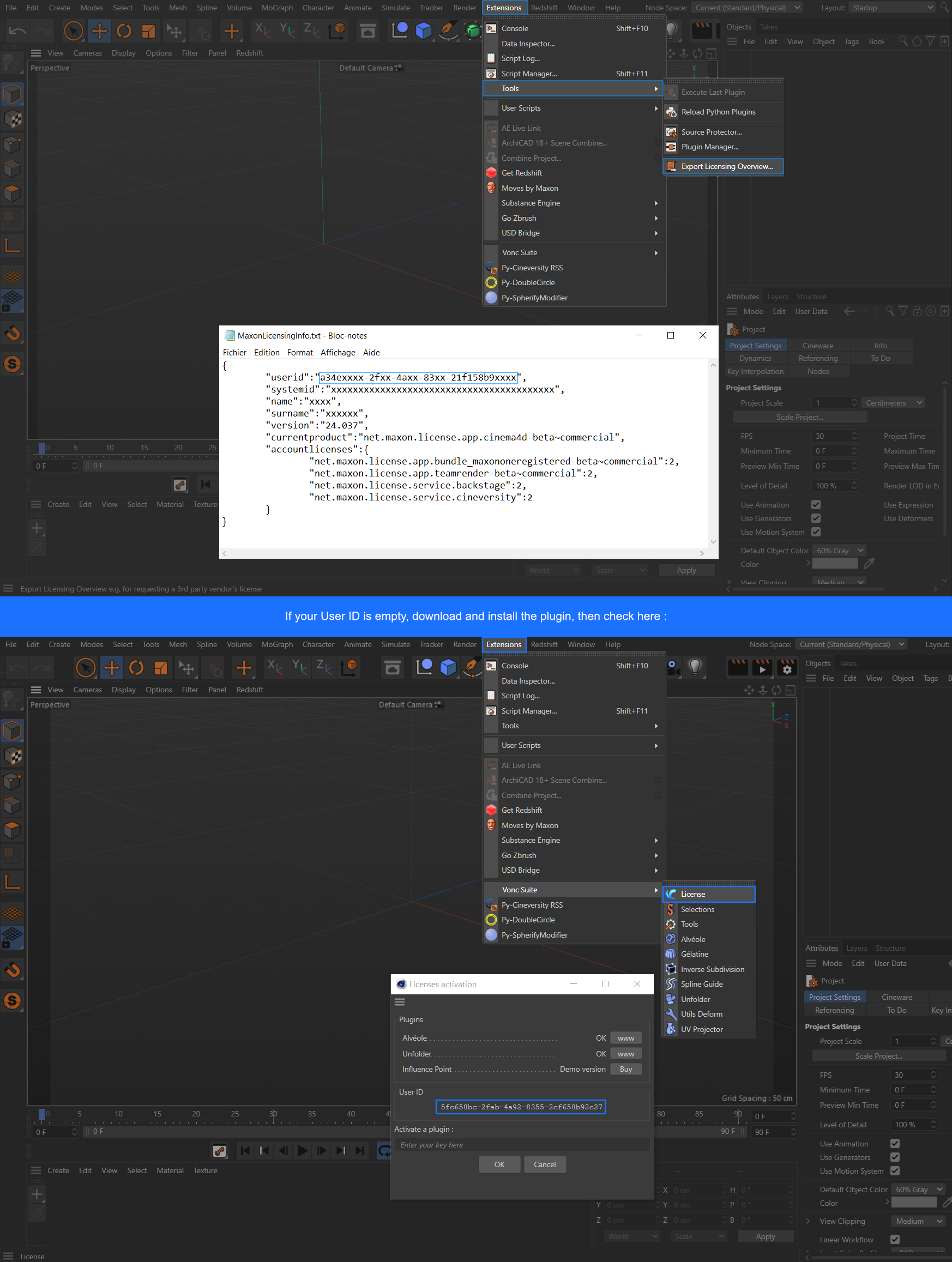
 Alvéole
Alvéole

 Projecteur UV
Projecteur UV

keyboard_arrow_down